
I have discovered teaching the language of math is significant to teaching math concepts and procedures. Students need to use correct mathematics terminology as vocabulary knowledge provides students with a mathematics foundation they can apply and build on whether they are in or out of the classroom. It really is all about the word, the right words! Since mathematical language is used and understood around the world, conventional mathematics vocabulary gives our students the means of communicating those concepts universally.
With that said, I have discovered that my college students
hate learning, reviewing or even practicing math vocabulary. I always begin the semester with a Mathematical Language Activity (see below) in which the students write two paragraphs about how they feel about the math language. You'd be surprised at how much I learn!
Even though my students have vocabulary assignments, and we play vocabulary games, especially before a test, many times they do it begrudgingly. Knowing that most of them like word puzzles, I created several math vocabulary crosswords to use in my classroom. The purpose of these puzzles is to have my students practice, review, recognize and use correct geometric vocabulary. I've made all of the crosswords free-form puzzles with the clues written in the form of definitions.
Often, I create two different puzzles for the same math vocabulary. The first puzzle is easier as it contains a word bank while the second puzzle does not. Since both puzzles are laid out differently, I can use one as a review and the second one as a homework assignment or maybe even as a quiz.
My newest crossword is on
circles. Both puzzles feature 18 terms associated with circles. The words showcased in both puzzles are arc, area, chord, circle, circumference, degrees, diameter, equidistant, perimeter, pi, radii, radius, secant, semicircle, tangent and two.
Also available are crosswords on
polygons (includes 16 geometric shapes with an emphasis on quadrilaterals and triangles),
plain geometry (features 25 different geometry terms with an emphasis on points, lines, and angles), and
solid geometry (emphasizes polyhedrons, circles, and formulas for area, surface area, and volume).
To keep my old gray matter working, I do the paper crossword every Sunday. To many of our students, math is like a puzzle, but maybe they can learn to love figuring out the puzzle by doing these crosswords. Why not give one a try in your classroom?
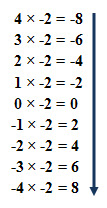 Let's examine 4 x -2 which means four sets of -2. Using the number line above, start at zero and move left by twos, four times. Voila! The answer is -8. Locate -8 on the number line above.
Let's examine 4 x -2 which means four sets of -2. Using the number line above, start at zero and move left by twos, four times. Voila! The answer is -8. Locate -8 on the number line above.

