When Dividing, Zero Is No Hero - Why We Can't Divide by Zero

Have you ever wondered why we can't divide by zero?  I remember asking that long ago in a math class, and the teacher's response was, "Because we just can't!"  I just love it when things are so clearly explained to me. So instead of a rote answer, let's investigate the question step-by-step.

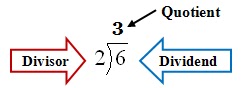
The first question we need to answer is what does a does division mean?  Let's use the example problem on the right.

1. The 6 inside the box means we have six items such as balls. (dividend) 
2. The number 2 outside the box (divisor) tells us we want to put or separate the six balls into two groups. 
3. The question is, “How many balls will be in each group?” 
4. The answer is, “Three balls will be in each of the two groups.” (quotient)

                                      

Using the sequence above, let's look at another problem, only this time let's divide by zero.

1. The 6 inside the box means we have six items like balls. (dividend) 
2. The number 0 outside the box (divisor) tells us we want to put or separate the balls into groups into no groups. 
3. The question is, “How many balls can we put into no groups?” 
4. The answer is, “If there are no groups, we cannot put the balls into a group.” 
5. Therefore, we cannot divide by zero because we will always have zero groups (or nothing) in which to put things. You can’t put something into nothing.

Let’s look at dividing by zero a different way. We know that division is the inverse (opposite) of multiplication; so………..

1. In the problem 12 ÷ 3 = 4.  This means we can divide 12 into three equal groups with four in each group.
2. Accordingly, 4 × 3 = 12.  Four groups with three in each group equals 12 things.

So returning to our problem of six divided by zero..... 

1. If 6 ÷ 0 = 0....... 
2. Then 0 × 0 should equal 6, but it doesn’t; it equals 0. So in this situation, we cannot divide by zero and get the answer of six.

We also know multiplication is repeated addition; so in the first problem of 12 ÷ 3, if we add three groups of 4 together, we should get a sum of 12. 4 + 4 + 4 = 12

As a result, in the second example of 6 ÷ 0, if six zeros are added together, we should get the answer of 6. 0 + 0 + 0 + 0 + 0 + 0 = 0 However we don’t. We get 0 as the answer; so, again our answer is wrong.

FREE

It is apparent that how many groups of zero we have is not important because they will never add up to equal the right answer. We could have as many as one billion groups of zero, and the sum would still equal zero. So, it doesn't make sense to divide by zero since there will never be a good answer. As a result, in the Algebraic world, we say that when we divide by zero, the answer is undefined. I guess that is the same as saying, "You can't divide by zero," but now at least you know why.

If you would like a free resource about this very topic, just click under the resource title page on your right.

Domino Math - Using Dominoes to Problem Solve and Practice Math Concepts

Dots Fun for Everyone

It is believed dominoes evolved from dice. In fact, the numbers in a standard double-six set of dominoes represent all the rolls of two six-sided die. It is thought they originated in China around the 12th century. They have been used in a large variety of games for hundreds of years, and today, dominoes are played all over the world.

Games allow children to learn a great deal concerning mathematical concepts and number relationships. Often, they are required to use critical thinking skills as well as varied math strategies to solve them. Since dominoes make a great manipulative for hands-on learning, I created a book of domino activities for grades 3-5 that are great for students who finish early or for introducing a new mathematical concept or for use at a math center. Using dominoes for a math practice center is a way to engage students while giving them a chance to review math facts.

The activities and three games vary in difficulty; so, differentiated instruction is easy. The variety of pages allows you to choose the practice page that is just right for each student. This resource correlates well with the CCSS standards.

Dots Fun

The activities in Dots Fun for Everyone (grades 3-5) include four digit place value, using the commutative property, problem solving, reducing proper and improper fractions and practicing multiplication and division facts. The games involve finding sums, using <, >, and = signs and ordering fractions.

These domino math activities in Dots Fun (primary grades) include recognizing sets, place value of two and four digit numbers, creating domino worms, gathering data, using the commutative property, and practicing addition and subtraction facts. The games involve matching, finding sums, and using greater than, less than, and equal signs. For these 13 activities and four games, you may use commercial sets dominoes or copy the blackline which is provided in the resource. This resource links closely with the CCSS standards. 

Some of the domino activities in these two resources use games while others will extend, enhance or introduce a new math concept. Since children are curious and inquisitive, plus some may have never seen dominoes, allow time for play and exploration before beginning any instruction. This is constructive as well as a productive use of class time. If they are not given this, most children will fool around and investigate during the teaching time.

To view examples from these resources as well as a complete Table of Contents, download the preview or FREE versions available at my TPT store.

You are invited to the Inlinkz link party!

Click here to enter