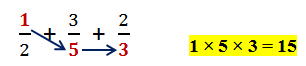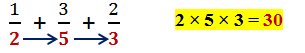Happy Pumpkin Day!

Hey, a little math humor, even on Halloween, can be "ghoul"!

 

 

 

Problem Solving Strategies

My math classes have been looking at different problem solving strategies, trying them out, and discovering what works best individually.  We've tried:

1. Using Models or Manipulatives
2. Drawing a Picture
3. Acting it Out or Role Playing
4. Making a Chart or Table
5. Making a List or a Graph
6. Looking for Patterns (All math is based on patterns.)
7. Working Backwards
8. Guessing and Checking
9. Making the Problem Simpler

I believe problem solving should be the central focus of any mathematics curriculum.  It is the major reason for studying math and provides a context in which concepts and skills can be learned.  It is the major vehicle for developing higher order thinking skills.  However, there is one problem solving strategy that will not work, although many students try it. This non-strategy poster hangs in my classroom.

 
Need some problem solving activities that are enjoyable, offer variety, and increase interest?  Think Tank Questions is a 14 page handout that contains 46 various questions.  Most subject areas are included in the questions which are appropriate for grades 2-6.

Fraction Action

In my July 1, 2011 posting entitled Fractions for the Confused and Bewildered, I introduced you to an alternate method for adding fractions called Cross Over, but sometimes students may have to add more than two fractions.  What happens then?  Let’s suppose we have the following problem.

Start out by multiplying the numerator of the first fraction by the denominators of the other two fractions as shown above.  (1 × 5 × 3 = 15)

Do the exact same thing with the second fraction and then add that product to the first.

Now repeat this process using the last numerator of 2 and add that to 33.

  

The result is the numerator of the answer.  To find the denominator, just multiply all the denominators together just as we do in the Cross Over strategy.

 

 

As usual, you may need to reduce to lowest terms or change an improper fraction to a mixed number.  In this example, the improper fraction becomes a mixed number.

For many of us, this may seem like a lengthy and complicated process but for my mathphobic students who have difficulty finding the lowest common denominator, they view this as easy and stress free.  The key is that they have a strategy that works for them.

If you are interested in other alternate ways to teach fractions, check out the resource Fractions for the Confused and Bewildered.

 

Teachers Pay Teachers - A Million Dollar Marketplace!

 

Did you read about our top TPT seller Deanna Jump who has reached the $1,000,000 mark by selling her products on Teachers Pay Teachers?  Yes, I did write the correct number of zeroes.  The TPT community is so very proud of her and this unbelievable accomplishment.  You can read about it yourself at:

http://www.abcactionnews.com/dpp/news/education/teacher-deanna-jump-makes-one-million-dollars-selling-school-lesson-plans 

You can also watch her TV interview by CNN at http://www.cbsnews.com/video/watch/?id=50133084n&tag=showDoorSubcatGrid%3BmorningSubCatAsset#

I want to sing the praises of TeachersPayTeachers; so, everyone knows why so many people love this site.   Here are a few of my favorite things... (Can't you hear me singing that song?  Okay, I'm not as good as Julie Andrews.)

1. It is a way to connect with other creative teachers; to share ideas, and to learn from others.
2. The site allows teachers to sell their products, while making 85% of the selling price. (If you have the premium membership.) Extra money is always good!
3. It exposes you to teachers from other states, even countries! 
4. It connects you with other educational blogs that in turn, make your job of teaching easier.

Why don't you join and become a seller?  It is easy to set up an account, and it's free!  Click on the blue letters to go to the home page.    Home Page of TPT

 

See You Later Alligator

I had posted this article back on May of 2011, but as I view products on Pinterest, I feel a need to revisit it.  I've seen alligators, fish, movable Popsicle sticks, etc. as ways to teach greater than or less than.   Even though these are a good visual tools, to be honest, there are no alligators or even fish in mathematics. 

 

Because many students still fail to understand this concept, here is a different approach which you might wish to try.   First of all, every child knows how to connect dots.  So let’s use that approach. 

 

Suppose we have two numbers 8 and 3.  Ask the students, “Which number is greater?"  Yes, 8 is greater.  Let’s put two dots beside that number.   8 :   Now ask, “Which number is smaller or represents the least amount?"  You are right again.  Three is smaller.  Let’s put one dot beside (in front of) that number.  Now have the students connect the dots.....

 

8 > 3    

 

It will work every time! When two numbers are equal, put two dots beside each number and connect the dots to make an equal sign.

What makes this method a little different is that the students can visually see which number is greater because it has the most dots beside it; so when reading the number sentence, it is usually read correctly.   

In a free handout, entitled Number Tiles - Activities for the Primary Grades, is a greater than and less than activity which can be used over and over again.  Just click on the blue title for your free copy.