In my July 1, 2011 posting entitled
Fractions for the Confused and Bewildered, I introduced you to an alternate
method for adding fractions called Cross Over, but sometimes students may have to
add more than two fractions. What happens
then? Let’s suppose we have the
following problem.
Start out by multiplying the numerator of the first fraction by the denominators of the other two fractions as shown above. (1 × 5 × 3 = 15)
Do the exact same thing with the second fraction and then add that product to the first.
Now repeat this process using the last numerator of 2 and add
that to 33.
The result is the numerator of the answer. To find the denominator, just multiply all
the denominators together just as we do in the Cross Over strategy.
As usual, you may need to reduce to
lowest terms or change an improper fraction to a mixed number. In this example, the improper fraction becomes
a mixed number.
For many of us, this may seem like a
lengthy and complicated process but for my mathphobic students who have
difficulty finding the lowest common denominator, they view this as easy and
stress free. The key is that they have a
strategy that works for them.
If you are interested in other alternate ways to teach fractions, check out the resource Fractions for the Confused and Bewildered.

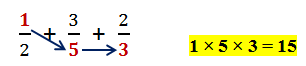


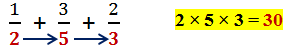


No comments:
Post a Comment