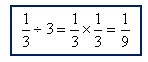Using Crossword Puzzles to Study The Christmas Story as Recorded in the Bible

$2.80

We may consider the Christmas tradition of reading the Nativity story a given, but after hearing others talk, it often gets overlooked in the hustle and bustle of opening gifts and preparing a big meal. The Christmas Story helps children discover one of the most important stories of all time. Through this story, children come to understand the events leading up to Jesus' birth and this special miracle. It introduces children to the reason why we celebrate this special day, and shares with them the wonderful gift from God. 

I am aware there are numerous Christmas activities to choose from and many times, it is difficult to separate the "secular" Christmas activities from the Biblical ones. Maybe you are wondering, "What activity can I use to tell the Christmas Story in a different way?" Try using a crossword puzzle! 

I have created two Bible crossword puzzles for Christmas that are specifically designed to review and study the birth of Christ as recorded in the Bible. Both are free form crossword puzzles that feature 25 words with Scripture references. If an answer is unknown, the Bible reference provides a way to find the answer while encouraging the use of the Bible. The words included in both puzzles are Bethlehem, Caesar Augustus, December, east, Egypt, Elizabeth, frankincense, Gabriel, glory, gold, Jesus, Joseph, King Herod, magi, manger, Mary, Merry Christmas, Messiah, myrrh, Nazareth, Quirinius, save, shepherds, star, and terrified.

One crossword includes a word bank which makes it easier to solve while the more challenging one does not. Even though the same words are used for each crossword, each grid is laid out in a different way; so, you have two distinct puzzles. Here are some ways you might use these crosswords.

1. Pass them out while the children are waiting to open presents. It might change their focus!
2. Include the adults in the puzzle solving by giving them the crossword without the word bank.
3. Work with a sibling or cousin or friend to learn the characters of the Christmas story.
4. Use the crossword with the word bank as a review; then hand out the second puzzle to solve as a way to reflect on what facts about Christmas have been learned.
5. Offer a small prize to the teams or individuals that get all off the answers correct.

Answers keys for both puzzles are included; so, you don't have to search them out yourself.

How to Overcome Mathphobia (a hatred of Math) and Be a Success

I HATE Math!

We are almost at the end of the fall semester at the college where I teach. (I teach Mathphobics who aren't always thrilled to be in my math class.) Last week, as the students were entering and finding seats, I was greeted with, “Math is my worst enemy!” I guess this particular student was waiting for an impending Math Attack. But then I began thinking, “Should this student wait to be attacked or learn how to approach and conquer the enemy?” Since winning any battle requires forethought and planning, here is a three step battle plan for Mathphobics.

1) Determine why math is your enemy. Did you have a bad experience? Were you ever made to feel stupid, foolish, or brainless? Did your parents say they didn’t like math, and it was a family heredity issue? (One of the curious characteristics about our society is that it is now socially acceptable to take pride in hating mathematics. It’s like wearing a badge of honor or is that dishonor? Who would ever admit to not being able to read or write?) Math is an essential subject and without math, not much is possible...not even telling time!

2) Be optimistic. Suffering from pessimism when thinking of or doing math problems makes it impossible to enjoy math. Come to class ready to learn. At the end of class, write down one thing you learned or thought was fun. I realize math teachers are a big part of how a student views math. In fact, one of the most important factors in a student’s attitude toward mathematics is the teacher and the classroom environment. Just using lecture, discussion, and seat work does not create much interest in mathematics. You've been in that class. Go over the homework; do samples of the new homework; start the new homework. Hands-on activities, songs, visuals, graphic organizers, and connecting math to real life engage students, create forums for discussion, and make math meaningful and useful.

3) Prove Yourself. Take baby steps, but be consistent. Faithfully do the homework and have someone check it. Don’t miss one math class! You can’t learn if you aren't there. Join in the discussions. Think about and write down your questions and share them with your teacher or with the class. Study for an upcoming test by reviewing 15 minutes each night a week before the test. Get help through tutoring, asking your instructor, or becoming a part of a study group. Keep in mind, no one is destined for defeat!

So don’t just sit there and wait for the dreaded Math Attack. Meet it head on with a three step battle plan in hand!
-------------------------------------------------------------------------------

FREE

Math courses are not like other courses. To pass most other subjects, a student must read, understand, and recall the subject matter. However, to pass math, an extra step is required: a student must use the information they have learned to solve math problems correctly. Special math study skills are needed to help the student learn more and to get better grades. To receive 20 beneficial math study tips, just download this free resource.

You are invited to the Inlinkz link party!

Click here to enter

Elvis and PEMDAS - A New Way to Introduce the Order of Operations

Any math teacher who teaches the Order of Operations is familiar with the phrase, "Please Excuse My Dear Aunt Sally".  For the life of me, I don't know who Aunt Sally is or what she has done, but apparently we are to excuse her for the offense.  In my math classes, I use "Pale Elvis Meets Dracula After School".  Of course both of these examples are mnemonics or acronyms; so, the first letter of each word stands for something.  P = Parenthesis, E = Exponents, M = Multiplication, D = Division, A = Addition, and S = Subtraction. 

I have always taught the Order of Operations by just listing which procedures should be done first and in the order they were to be done.  But after viewing a different way on Pinterest, I have changed my approach. Here is a chart with the details and the steps to "success" listed on the right.

Since multiplication and division as well as addition and subtraction equally rank in order, they are written side by side. What I like about this chart is that it clearly indicates to the student what they are to do and when.  To sum it up:

When expressions have more than one operation, follow the rules for the Order of Operations:

1. First do all operations that lie inside parentheses.
2. Next, do any work with exponents or radicals.
3. Working from left to right, do all the multiplication and division.
4. Finally, working from left to right, do all the addition and subtraction.

Failure to use the Order of Operations can result in a wrong answer to a problem.  This happened to me when I taught 3rd grade.  On the Test That Counts, the following problem was given.

The correct answer is 11 because you multiply the 4 x 2 and then add the 3, but can you guess which answer most of my students chose?  That's right - 14!  From that year on, the Order of Operations became a priority in my classroom.  Is it a priority in yours?  Should it be?

-----------------------------------------------------------------------------

$3.75

I have a product in my store entitled: Order of Operations - PEMDAS, A New Approach. This ten page resource includes a lesson plan outline for introducing PEMDAS, an easy to understand chart for the students, an explanation of PEMDAS for the student as well as ten practice problems. It is aligned with the fifth grade common core standard of 5.OA.1. Just click on the words under the cover page if it is something you might like.

October - Is It "Fall" or "Autumn"? Doing Science Investigations Using Leaves

October has finally arrived.  October means football (Ohio State, of course), cooler weather, and gorgeous leaves. (It is also the month my husband and I were married.) In October, we see the leaves turning colors, and the deciduous trees shedding their leaves.

Another name for fall is autumn, a rather strange name to me. Through research, I discovered that the word autumn is from the Old French autumpne, automne, which came from the Latin autumnus. Autumn has been in general use since the 1960's and means the season that follows summer and comes before winter.

Fall is the most common usage among those in the United States; however, the word autumn is often interchanged with fall in many countries including the U.S.A. It marks the transition from summer into winter, in September if you live in the Northern Hemisphere or in March if you live in the Southern Hemisphere.  It also denotes when the days are noticeably shorter and the temperatures finally start to cool off. In North America, autumn is considered to officially start with the September equinox. This year it was on September 23rd.

With all of that said, the leaves in our neighbor's yard have already begun to fall into ours which aggravates my husband because he is the one who gets to rake them. Maybe focusing on some activities using leaves will divert his attention away from the thought of raking leaves to science investigations.  

Remember ironing leaves between wax paper?  We did that in school when I was a little girl (eons and eons ago).  Here is how to do it.

1. Find different sizes and colors of leaves.
2. Tear off two sheets about the same size of waxed paper.
3. Set the iron on "dry".  No water or steam here!
4. The heat level of the iron should be medium.
5. Place leaves on one piece of the waxed paper.
6. Lay the other piece on top.
7. Iron away!

You can also use this activity to identify leaves.  According to my husband who knows trees, leaves and birds from his college studies, we "waxed" a maple leaf, sweet gum leaf, elm leaf, cottonwood leaf (the state tree of Kansas - they are everywhere), and two he doesn't recognize because they come from some unknown ornamental shrubs.

$5.30

Maybe you would like to use leaves as a science investigation in your classroom.  I have one in my Teacher Pay Teachers store that is a six lesson science performance demonstration for grades K-2. The inquiry guides the primary student through the scientific method and includes: 

1. Exploration time
2. Writing a good investigative question
3. Making a prediction
4. Designing a plan
5. Gathering the data
6. Writing a conclusion based on the data. 

Be"leaf" me, your students will have fun!

Terrible at Factoring Trinomials (Polynomials) in Algebra? Try This Method that NEVER Fails!

I spent the summer months tutoring a high school girl who was getting ready to take Algebra II.  She didn't do very well in Algebra I and with geometry between the two classes, she was lost. Since she is a very concrete, visual person, I knew I needed to come up with different algebraic methods so she could succeed. 

When we got to to factoring trinomials, she really needed help as most of the methods were too abstract for her. For those of you who have forgotten, a trinomial is a polynomial that has three terms. Most likely, students start learning how to factor trinomials written in the form ax² + bx + c. 

There are several different methods that can be used to factor trinomials.  The first is guess and check using ac and grouping. Find two numbers that ADD up to b and MULTIPLY to get ac in ax² + bx + c. The second approach is the box method. You write the equation in a two-by-two box. This method is more thoroughly explained on You Tube. Look up factoring trinomials using the box method.  There is also the method of slide and divide which again you can look up on You Tube to see exactly how that works. Grouping is another method. Students need to choose which method they understand and which one works best for them. With continual practice, they will get better and faster at using it.

My favorite method is the one most students understand and grasp. It builds on the ac method, but takes it takes it one step further. It made sense to my student, and she was easily factoring trinomials after only two tutoring sessions.

Because it worked so well, I developed a new math resource. It is a step-by-step guide that teaches how to factor quadratic equations in a straightforward and uncomplicated way. It includes polynomials with common monomial factors, and trinomials with and without 1 as the leading coefficient. Some answers are prime. This simple method does not treat trinomials when a =1 differently since those problems are incorporated with “when a is greater than 1” problems.

Following each explanation (five total) are a set of six practice problems that replicate the method introduced. You might familiarize the students with the method, then assign the problems to practice, OR you might present all four explanations, and then assign the practice problems to review. Some students will catch on rapidly and will not need to go through all of the steps while others will need more repetition and practice. Differentiate your instruction accordingly. Try working in pairs or small groups since students tend to learn from each other.

-----------------------------------------------------------------------------

$5.25

Included in this resource are the following:

• A detailed explanation of this factoring method.
  
• Five variations when using this method
• Five sets of practice problems – 30 in total
• Two sets of review problems – 12 total
• Answers Keys with the complete problem-solving process

If your students don't understand FOIL, Try Multiplying Binomials Using the Box Method

I tutored a student this summer who was getting ready to take Algebra II. He is a very visual, concrete person that needs many visuals to help him to succeed in math. We worked quite a bit on multiplying two binomials.

There are three different techniques you can use for multiplying polynomials. You can use the FOIL method, Box Method and the distributive property. The best part about it is that they are all the same, and if done correctly, will render the same answer.!

Because most math teachers start with FOIL, I started there. The letters FOIL stand for First, Outer, Inner, Last. First means multiply the terms which occur first in each binomial. Then Outer means multiply the outermost terms in the product. Inner is for "inside" so those two terms are multiplied—second term of the first binomial and first term of the second). Last is multiplying the last terms of each binomial.

My student could keep FOIL in his head, but couldn't quite remember what the letters represented, let alone which numbers to multiply; so, that method was quickly laid aside. 

I next tried the Box Method. Immediately, it made sense to him, and we were off to the races, so to speak. He continually got the right answer, and his confidence level continued to increase. Here is how the Box Method works.

First, you draw a 2 x 2 box. Second, write the binomials, one along the top of the box, and one binomial down the left hand side of the box. Let's assume the binomials are 2x + 4 and x + 3.

          (2x + 4) (x + 3)

Now multiply the top row by x; that is x times 2x and x times +4., writing the answers in the top row of the box, each in its own square.  After that, multiply  everything in the top row by +3, and write those answers in the second row of the box, each in its own square.

Looking at the box, circle the coefficients that have an x. They are located on the diagonal of the box.

To find the answer, write the term in the first square on the top row, add the terms on the diagonal, and write the number in the last square on the bottom row. Voila! You have your answer!

Algebra - Using Two-Sided Colored Beans to Add and Subtract Positive and Negative Numbers

When it comes to adding and subtracting positive and negative numbers, many students have great difficulty. In reality, it is a very confusing and abstract idea; so, it is important to give the students a concrete visual to assist them in seeing the solution. This idea is based on the Conceptual Development Model which is important to use when introducing new math concepts. (See the July 26, 2023 for more details about this learning model.) As a result, when teaching the concept of adding and subtracting positive and negative numbers, what would fall into each category?

When using the two-sided colored beans, the concrete stage of the Model would be where two-sided colored beans are used as an actual manipulative that can be moved around or manipulated by the students. There are a few rules to remember when using the beans.

1. The RED beans represent negative numbers.
2. The WHITE beans represent positive numbers. 
3. One RED bean can eliminate one WHITE bean, and one WHITE bean can cancel out one RED bean. 
4. All problems must be rewritten so that there is only one sign (+ or -) in front of each number.

Sample Problem

1) The student is given the problem - 5 + 2.

2) Since -5 is negative, the student gets out five red beans, and then two white beans because the 2 is positive.

3) Since some of the beans are red and two are white, the student must match one red bean with one white bean. (I tell my students that this is barbaric because the red beans eat the white beans. They love it!)

4) Because three red beans have no partner (they're left over) the answer to – 5 + 2 = - 3. (See example above.)

After mastering the concrete stage of the Conceptual Development Model, the students would move on to the pictorial stage. Sketching a picture of the beans would be considered pictorial. Have students draw circles to represent the beans, leaving the circles that denote positive numbers white and coloring the circles that represent negative numbers red.

As an example, let’s do the problem 3 - +5. First, rewrite the problem as 3 - 5. Now draw three white beans. Draw five more beans and color them red to represent -5. Match one white bean to one red bean. Two red beans are left over; therefore, the answer to 3 - +5 is -2.

3 - +5 = 3 – 5 = -2 

When students understand the pictorial stage, then abstract problems such as the ones in textbooks can be presented. (Notice, the textbook is the last place we go for an introduction.) I have found that most of my remedial college students move straight from the concrete stage (beans) to the abstract stage without any problem. Many put away the beans after two or three lessons. What works best for your students as they master this algebraic concept is something you will have to determine.

$5.35

If you would like a resource that gradually goes through these lessons, you can purchase it on Teachers Pay Teachers. It introduces the algebraic concept of adding and subtracting positive and negative numbers and contains several integrated hands-on activities. They include short math lessons with step-by-step instructions on how to use the beans, visual aids and illustrations, four separate and different practice student worksheets with complete answers in addition to detailed explanations for the instructor.

You are invited to the Inlinkz link party!

Click here to enter

Skip Counting and Learning How to Multiply Using Pattern Sticks

Most elementary teachers use a Hundreds Board in their classroom.  It can be used for introducing number patterns, sequencing, place value and more. Students can look for counting-by (multiplication) patterns. Colored disks, pinto beans or just coloring the squares with crayons or colored pencils will work for this. Mark the numbers you land on when you count by two. What pattern do they make? Mark the counting-by-3 pattern, or mark the 7's, etc. You may need to print several charts so your students can color in the patterns and compare them. I usually start with the 2's, 5's and 10's since most children have these memorized.

On the other hand, the Hundreds Board can also be confusing when skip counting because there are so many other numbers listed which easily create a distraction.  I have found that Pattern Sticks work much better because the number pattern the student is skip counting by can be isolated. Pattern Sticks are a visual way of showing students the many patterns that occur on a multiplication table.  Illustrated below is the pattern stick for three. As the student skip counts by three, s/he simply goes from one number to the next (left to right).

Martian Fingers

For fun, I purchase those scary, wearable fingers at Halloween time. (buy them in bulk from The Oriental Trading Company - click under the fingers for the link.) Each of my students wears one for skip counting activities. I call them the Awesome Fingers of Math! For some reason, when wearing the fingers, students tend to actually point and follow along when skip counting.

Most students enjoy skip counting when music is played. I have found several CD's on Amazon that lend themselves nicely to this activity.  I especially like Hap Palmer's Multiplication Mountain.  My grandchildren think his songs are catchy, maybe too catchy as sometimes I can't get the songs out of my mind!

$3.25

Think about this.  As teachers, if we would take the time to skip count daily, our students would know more than just the 2's, 5's and 10's.  They would know all of their multiplication facts by the end of third grade. And wouldn't the fourth grade teacher love you?!?

IMPORTANT:  If you like this finger idea, be sure that each student uses the same finger every time to avoid the spreading of germs. Keeping it in a zip lock bag with the child’s name on the bag works best. (Believe it or not, when I taught fourth grade, the students would paint and

decorate the fingernails!)

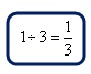
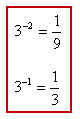
To help your students learn their multiplication facts, you might like the resource entitled Pattern Sticks. It is a a visual way of showing students the many patterns on a multiplication table. It also teaches how you to use the pattern sticks to recognize equivalent fractions, reduce fractions, and to change improper fractions to mixed numbers.

You're Teaching Fractions All Wrong! Don't Flip When You Divide!

My college students in remedial math just finished the chapter on fractions. Talk about mathphobia. Dividing fractions was the most confusing for them because it requires finding the reciprocal of the second fraction, changing the division sign to a multiplication sign, and then multiplying the numerator times the numerator and the denominator times the denominator.

Let me introduce a new method entitled "Just Cross".

First and foremost, you must understand what division is. The statement 8 ÷ 4 means 8 divided into 4 equal sets, OR how many fours are in eight, OR how many times can we subtract 4 from 8? (Yes, division is repeated subtraction.)

Let me explain this using a hands-on visual. Let’s assume the fraction problem is:

The question being asked is, “How many ¼’s are in ½?” 

First, fold a piece of paper in half. The figure on the left represents ½. Next, fold the same sheet of paper in half again to make fourths as seen in the illustration on the right. When you unfold the paper, you will notice a total of four sections. So answering the original question: “How many ¼’s are in ½”, you can see that the half sheet of paper contains two parts; therefore:

Using the same example, to work the problem, the fraction 1/4 would have to be flipped to 4/1 nd then 1/2 would have to multiplied by 4/1 to get the correct answer of 2. That is why the division of fractions requires that the second fraction be inverted and the division sign be changed to a multiplication sign.

Let’s use the same fraction problem, but let’s utilize a different method entitled Just Cross. 

• Cross your arms as a hands-on way of remembering the process.

• Now multiply the denominator of 4 by 1 the denominator of 2 by1 as seen below. (We do nothing with the denominators.) Notice we always start on the right side and then we go to the left side. If it is done the opposite way, the answer will be incorrect. The answer of our first "cross" is the numerator (4 x 1); the answer to our second "cross" (2x1) is the denominator.

• Now simply divide 4 by 2 to get the answer of 2.

No flipping; no reciprocal, no changing the division sign to a multiplication sign. Just Cross and divide. Amazingly, it works every time. 

-------------------------------------------------------------------------------

$4.75

Although fractions are something every student should learn, often times numerous students are left behind in the mathematical dust when a math textbook is followed page by page. I have a resource that features different ways to teach fractions using hands-on strategies similar to the one above. The unconventional techniques described in this math resource will always work.  Just go to Unlocking Fractions for the Confused and Bewildered.

Linking Literature and Math Using the Book, "Math Curse." It's the Perfect Book for the Beginning of the Year!

I love books that link math and literature, and one of my favorites is Math Curse by Jon Scieszka. Published in 1995 through Viking Press, the book tells the story of a student who is cursed by the way mathematics works in everyday life. It is a tale where everything is a math problem, from tabulating teeth to calculating a bowl of corn flakes. Everything in life becomes a math problem.

First you see the math teacher, Mrs. Fibonacci, (don’t you love that name?) declare, “You know, you can think of almost everything as a math problem.” Then you watch as the student turns into a “raving math lunatic” since s/he believes “Mrs. Fibonacci has obviously put a math curse on me.”

From sunrise to sunset, the student anxiously mulls over the answers to countless calculations such as: How much time does it take to get ready and be at the bus stop? (a problem the reader can solve.). Estimate how many M & M's you would eat if you had to measure the Mississippi River using M & Ms. There is even an English word problem: “If mail + box = mailbox, does lipstick – stick = lip? Does tunafish + tunafish = fournafish?” (silly, but funny.) A class treat of cupcakes becomes a study in fractions, while a trip to the store turns into a problem of money. The story continues until the student is finally free of the math curse, but then again Mr. Newton, the science teacher, regrettably says, “You know, you can think of almost everything as a science experiment.”

Math Curse is full of honest to goodness math problems (and some rather unrelated bonus questions, such as "What does this inkblot look like?"). Readers can try to solve the problems and check their answers located on the back cover of the book. The problems are perfect to get students’ minds working and thinking about how math really does apply to their everyday life.

The illustrations by Lane Smith are one of a kind. They are busy and chaotic to reflect the “math zombie” this student becomes. Many resemble a cut and paste project, with some images touching or overlapping others. Mostly dark colors are used especially when the student begins to dream s/he is trapped in a blackboard room covered with never-ending math problems. (a nightmare for many) Smith’s art work makes Scieszka's words come to life and helps to paint a picture of what is going through the mind of the main character as s/he deals with the dreaded math curse.

John Scieszka does a remarkable job of breaking down the typical school day into math problems while also adding some tongue-in-cheek and light hearted humor which every mathphobic needs. The math is perhaps a little advanced for elementary students, but the problems are perfect for middle school or high school students.

Math Curse also demonstrates how a problem may seem difficult, but if you are persistent, you can find the solution to the problem. The book teaches not to fear or be anxious about math or for that matter, any other subject in school. Despite the fact the main character is completely overwhelmed by mathematics, it allows students who struggle with the identical feeling to know they are not alone. Any student who has ever been distressed over numbers, fractions, word problems and the like will certainly identify with the main character.

As a math teacher, I think this book makes math fun as well as interesting. Although I recognize math is everywhere in everyday life, I never realized just how much until I read the Math Curse and mathematically saw the day of a typical student. I believe what sets Math Curse apart from other books is that it accurately illustrates and explains how math is actually used and applied in day-to-day life. I love the story, the message, and especially the content.

You are invited to the Inlinkz link party!

Click here to enter

How Many Classroom Management Rules Does A Teacher Really Need?

Now that most of us are getting geared up for a new school year, it's time to think about what classroom rules need to be established. Maybe the ones you had last year just didn’t work, and you are looking for a change. I could recommend many "Do this or this will happen" or "Please don't do this as it will break my heart" statements, but lists can become very long and mind-numbing. Maybe that is why God only gave Ten Commandments. Fewer rules mean less has to be memorized. So, maybe we need to ask ourselves: “How many classroom rules are really needed?” 

I would suggest making a few general rules that are clear and understandable since being too specific often leads to complicated, wordy rules that might cover every possible situation. Most of the time, I post six simple classroom rules (only two words each) in my room which encompass my main areas of concern. I find them to be more than sufficient to govern general behaviors, and because alliteration is used, the rules are easy for all of my students to remember.

1.  Be Prompt – In other words, be on time to school/class/group.

2.  Be Prepared – Bring the items you need to class or to a group. Study for upcoming tests. Have your homework completed and ready to turn in. 

3.  Be Polite – This rule focuses on how we treat each other. Show respect for your teacher(s) and your fellow students in the classroom, in the school, and on the playground.

4.  Be Persistent - The final rule spotlights the need to stay on task and complete an assignment even though it might be difficult. 

5. Be Productive - Always put forth your best effort! Grades are achieved; not received; so, do your best at all times.

6. Be Positive – Bad days happen! If you are having one of those days, I do understand. Please just inform me before class that you are having a bad day, and I will try to leave you alone during class discussion. This is not to be abused.

I firmly believe that class rules must cover general behaviors, be clear as well as understandable. Being too specific often leads to complicated, wordy rules that might cover every possible situation, but are impossible to remember.  (A good example are the IRS tax rules which I still have difficulty comprehending). 

Here are a few things to consider when communicating your classroom rules.

$2.60

• Establish clear expectations for behavior from day one.
• Use techniques such as interactive modeling to teach positive behavior.
• Reinforce positive behavior with supportive teacher language.
• Quickly stop misbehavior.
• Restore positive behavior so that children retain their dignity and continue learning.

If you are interested in using these six rules in your classroom, check them out on Teachers Pay Teachers. Each two word rule is written as a one page chart, and is ready to download and laminate to hang in your classroom.

Developing and Writing Effective Math Lesson Plans That Work!

We often hear of research based strategies and how to use them in our classrooms. Having worked at two colleges in the past 20 years, I have discovered that some who are doing this research have never been in a classroom or taught anyone under the age of 18!  (Sad but True)  Then there are others who truly understand teaching, have done it, and want to make it more effective for everyone. That's the kind of research I am anxious to use.  I came across the Conceptual Development Model while teaching a math methods class to future teachers. It was one of the first research models that I knew would work. 

The Conceptual Development Model involves three stages of learning: 1) concrete or manipulative, 2) pictorial, and 3) the abstract.  The concrete stage involves using hands-on teaching which might involve the use of math manipulatives or real items. Next, the pictorial stage utilizes pictures to represent the real objects or manipulatives. A visual such as a graphic organizer would also fit in this stage. Last, the abstract stage of development entails reading the textbook, using numbers to compute, solving formulas, etc. Let's look at two classroom examples.

Example #1:  You are a first grade teacher who is doing an apple unit.  You decide to have the children graph the apples, sorting them by color.

Concrete:  Using a floor graph, the children use real apples to make the graph.

Pictorial:  The children have pictures of apples that they color and then put on the floor graph.

Abstract:  The children have colored circles which represent the apples.

Example #2:  You are a fifth grade teacher who wants to teach how to find the volume of a cube or rectangular solid.

Concrete: Bring a large box into the classroom, a box large enough for the children to climb inside, OR have the students build 3-D objects using multi-link cubes.

Pictorial: Give the students pictures of 3D objects which are drawn but shows the cubes used to make the solid. Have the students count the cubes to determine the volume.

Abstract: Have students use the formula l x w x h to find volume.

Requiring my perspective teachers to think about this model and to use it when planning a math unit dramatically changed the quality of instruction which I observed in the classroom. 

$3.00

Now that I teach mathphobics on the college level, I am finding this model to be a crucial part of my planning.  Most of my students started math at the abstract level, "Open your books to page...." without any regard to the other two stages of development. Using manipulatives and graphic organizers have changed my students' ability to learn math, and some have even ended the semester by saying, "I like math". Maybe this is a model we should all consider implementing.

If you want more examples and suggestions about using this model to write math lesson plans, click on the resource cover. 

Also look at the resource entitled Graphing without Paper or Pencil in which is appropriate for grades K-5 and is based on the Conceptual Model of Development: concrete to pictorial to abstract.

When Multiplying Polynomials, FOIL Doesn't Always Work!

Using FOIL

In more advanced math classes, many instructors happen to hate "FOIL" (including me) because it only provides confusion for the students. Unfortunately, FOIL (an acronym for first, outer, inner and last) tends to be taught as THE way to multiply all polynomials, which is certainly not true. As soon as either one of the polynomials has more than a "first" and "last" term in its parentheses, the students are puzzled as well as off course if they attempt to use FOIL. If students want to use FOIL, they need to be forewarned: You can ONLY use it for the specific case of multiplying two binomials. You can NOT use it at ANY other time!

When multiplying larger polynomials, most students switch

to vertical multiplication, because it is much easier to use, but there is another way. It is called the clam method. (An instructor at the college where I teach says that each set of arcs reminds her of a clam. She’s even named the clam Clarence; so, at our college, this is the Clarence the Clam method.)

Let’s say we have the following problem:

(x + 2) (2x²  + 3x – 4)

Simply multiply each term in the second parenthesis by the first term in the first parenthesis. Then multiply each term in the second parenthesis by the second term in the first parenthesis.

I have my students draw arcs as they multiply. Notice below that the arcs are drawn so they connect to one another to designate that this is a continuous process. Begin with the first term and times each term in the second parenthesis by that first term until each term has been multiplied.

When they are ready to work with the second term, I have the students use a different color.  This time they multiply each term in the second parenthesis by the second term in the first while drawing an arc below each term just as they did before.  The different colors help to distinguish which terms have been multiplied, and they serve as a check point to make sure no term has been missed in the process.

As they multiply, I have my students write the answers horizontally, lining up the like terms and placing them one under the other as seen below. This makes it so much easier for them to add the like terms:

This "clam" method works every time a student multiplies polynomials, no matter how many terms are involved.

Let me restate what I said at the start of this post: "FOIL" only works for the special case of a two-term polynomial multiplied by another two-term polynomial. It does NOT apply to in ANY other case; therefore, students should not depend on FOIL for general multiplication. In addition, they should never assume it will "work" for every multiplication of polynomials or even for most multiplications. If math students only know FOIL, they have not learned all they need to know, and this will cause them great difficulties and heartaches as they move up in math.

Personally, I have observed too many students who are greatly hindered in mathematics by an over reliance on the FOIL method. Often their instructors have been guilty of never teaching or introducing any other method other than FOIL for multiplying polynomials. Take the time to show your students how to multiply polynomials properly, avoid FOIL, if possible, and consider Clarence the Clam as one of the methods to teach.